Multi-node Computation¶
Introduction¶
This chapter describes all base objects (matrices and vectors) for computation on multi-node (distributed memory) systems.
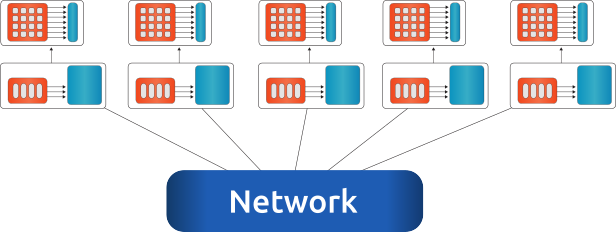
Fig. 3 An example for a multi-node configuration, where all nodes are connected via network. Single socket systems with a single accelerator.¶
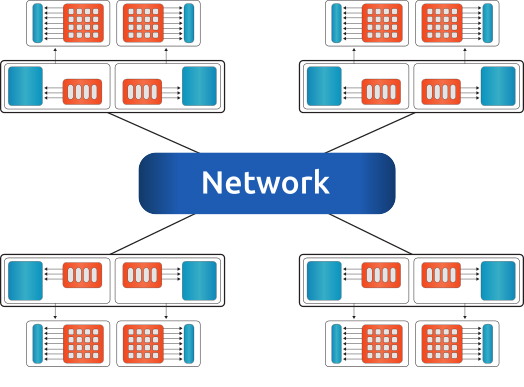
Fig. 4 An example for a multi-node configuration, where all nodes are connected via network. Dual socket systems with two accelerators attached to each node.¶
To each compute node, one or more accelerators can be attached. The compute node could be any kind of shared-memory (single, dual, quad CPU) system, details on a single-node can be found in Fig. 2.
Note
The memory of accelerator and host are physically different. All nodes can communicate with each other via network.
For the communication channel between different nodes (and between the accelerators on single or multiple nodes) the MPI library is used.
rocALUTION supports non-overlapping type of distribution, where the computational domain is split into several sub-domain with the corresponding information about the boundary and ghost layers. An example is shown in Fig. 5. The square box domain is distributed into four sub-domains. Each subdomain belongs to a process P0, P1, P2 and P3.

Fig. 5 An example for domain distribution.¶
To perform a sparse matrix-vector multiplication (SpMV), each process need to multiply its own portion of the domain and update the corresponding ghost elements. For P0, this multiplication reads
where \(I\) stands for interior and \(G\) stands for ghost. \(x_G\) is a vector with three sections, coming from P1, P2 and P3. The whole ghost part of the global vector is used mainly for the SpMV product. It does not play any role in the computation of vector-vector operations.
Code Structure¶
Each object contains two local sub-objects. The global matrix stores interior and ghost matrix by local objects. Similarily, the global vector stores its data by two local objects. In addition to the local data, the global objects have information about the global communication through the parallel manager.
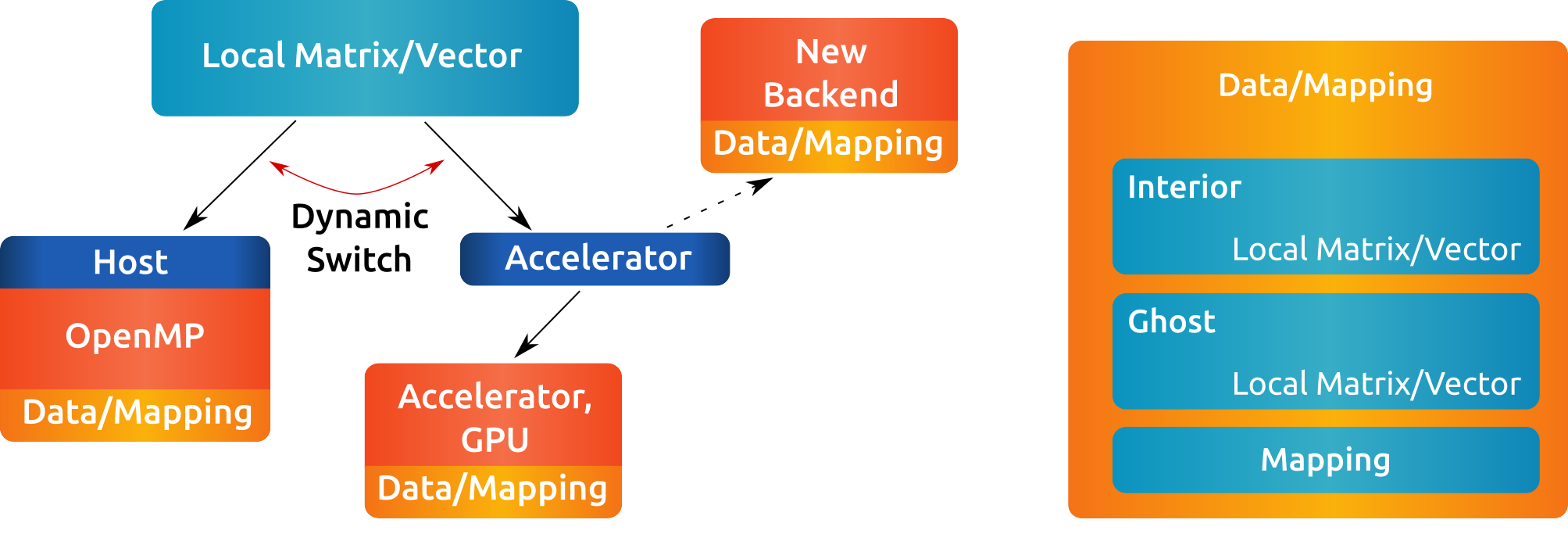
Fig. 6 Global matrices and vectors.¶
Parallel Manager¶
-
class ParallelManager : public rocalution::RocalutionObj
Parallel Manager class.
The parallel manager class handles the communication and the mapping of the global operators. Each global operator and vector need to be initialized with a valid parallel manager in order to perform any operation. For many distributed simulations, the underlying operator is already distributed. This information need to be passed to the parallel manager.
The parallel manager class hosts the following functions:
-
void rocalution::ParallelManager::SetMPICommunicator(const void *comm)
Set the MPI communicator.
-
void rocalution::ParallelManager::Clear(void)
Clear all allocated resources.
Warning
doxygenfunction: Cannot find function “rocalution::ParallelManager::GetGlobalSize” in doxygen xml output for project “rocALUTION” from directory: ../docBin/xml
Warning
doxygenfunction: Cannot find function “rocalution::ParallelManager::GetLocalSize” in doxygen xml output for project “rocALUTION” from directory: ../docBin/xml
-
int rocalution::ParallelManager::GetNumReceivers(void) const
Return the number of receivers.
-
int rocalution::ParallelManager::GetNumSenders(void) const
Return the number of senders.
-
int rocalution::ParallelManager::GetNumProcs(void) const
Return the number of involved processes.
Warning
doxygenfunction: Cannot find function “rocalution::ParallelManager::SetGlobalSize” in doxygen xml output for project “rocALUTION” from directory: ../docBin/xml
Warning
doxygenfunction: Cannot find function “rocalution::ParallelManager::SetLocalSize” in doxygen xml output for project “rocALUTION” from directory: ../docBin/xml
-
void rocalution::ParallelManager::SetBoundaryIndex(int size, const int *index)
Set all boundary indices of this ranks process.
-
void rocalution::ParallelManager::SetReceivers(int nrecv, const int *recvs, const int *recv_offset)
Number of processes, the current process is receiving data from, array of the processes, the current process is receiving data from and offsets, where the boundary for process ‘receiver’ starts.
-
void rocalution::ParallelManager::SetSenders(int nsend, const int *sends, const int *send_offset)
Number of processes, the current process is sending data to, array of the processes, the current process is sending data to and offsets where the ghost part for process ‘sender’ starts.
-
void rocalution::ParallelManager::ReadFileASCII(const std::string &filename)
Read file that contains all relevant parallel manager data.
-
void rocalution::ParallelManager::WriteFileASCII(const std::string &filename) const
Write file that contains all relevant parallel manager data.
To setup a parallel manager, the required information is:
Global size
Local size of the interior/ghost for each process
Communication pattern (what information need to be sent to whom)
Global Matrices and Vectors¶
-
const LocalMatrix<ValueType> &rocalution::GlobalMatrix::GetInterior() const¶
-
const LocalMatrix<ValueType> &rocalution::GlobalMatrix::GetGhost() const¶
Warning
doxygenfunction: Unable to resolve function “rocalution::GlobalVector::GetInterior” with arguments None in doxygen xml output for project “rocALUTION” from directory: ../docBin/xml. Potential matches:
- LocalVector<ValueType> &GetInterior()
- const LocalVector<ValueType> &GetInterior() const
The global matrices and vectors store their data via two local objects. For the global matrix, the interior can be access via the rocalution::GlobalMatrix::GetInterior() and rocalution::GlobalMatrix::GetGhost() functions, which point to two valid local matrices. Similarily, the global vector can be accessed by rocalution::GlobalVector::GetInterior().
Asynchronous SpMV¶
To minimize latency and to increase scalability, rocALUTION supports asynchronous sparse matrix-vector multiplication. The implementation of the SpMV starts with asynchronous transfer of the required ghost buffers, while at the same time it computes the interior matrix-vector product. When the computation of the interior SpMV is done, the ghost transfer is synchronized and the ghost SpMV is performed. To minimize the PCI-E bus, the HIP implementation provides a special packaging technique for transferring all ghost data into a contiguous memory buffer.
File I/O¶
The user can store and load all global structures from and to files. For a solver, the necessary data would be
the parallel manager
the sparse matrix
and the vector
Reading/writing from/to files can be done fully in parallel without any communication. Fig. 7 visualizes data of a \(4 \times 4\) grid example which is distributed among 4 MPI processes (organized in \(2 \times 2\)). Each local matrix stores the local unknowns (with local indexing). Fig. 8 furthermore illustrates the data associated with RANK0.
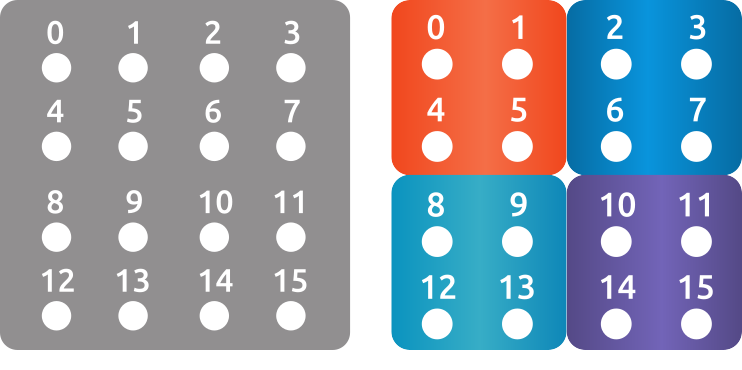
Fig. 7 An example of \(4 \times 4\) grid, distributed in 4 domains (\(2 \times 2\)).¶
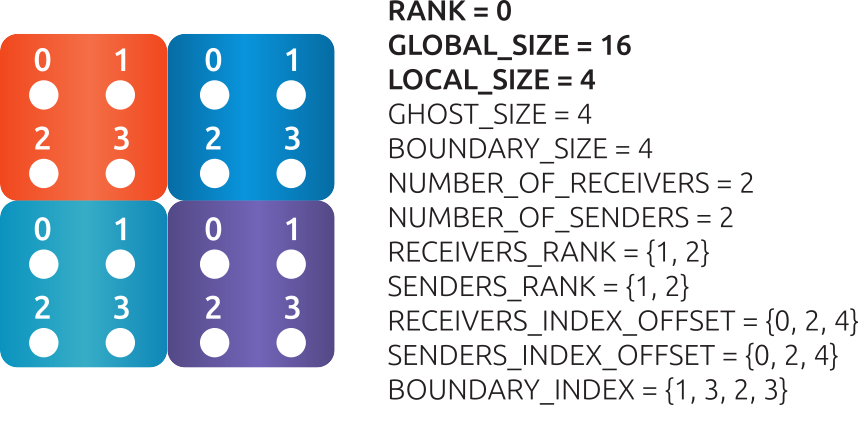
Fig. 8 An example of 4 MPI processes and the data associated with RANK0.¶
File Organization¶
When the parallel manager, global matrix or global vector are writing to a file, the main file (passed as a file name to this function) will contain information for all files on all ranks.
parallelmanager.dat.rank.0
parallelmanager.dat.rank.1
parallelmanager.dat.rank.2
parallelmanager.dat.rank.3
matrix.mtx.interior.rank.0
matrix.mtx.ghost.rank.0
matrix.mtx.interior.rank.1
matrix.mtx.ghost.rank.1
matrix.mtx.interior.rank.2
matrix.mtx.ghost.rank.2
matrix.mtx.interior.rank.3
matrix.mtx.ghost.rank.3
rhs.dat.rank.0
rhs.dat.rank.1
rhs.dat.rank.2
rhs.dat.rank.3
Parallel Manager¶
The data for each rank can be split into receiving and sending information. For receiving data from neighboring processes, see Fig. 9, RANK0 need to know what type of data will be received and from whom. For sending data to neighboring processes, see Fig. 10, RANK0 need to know where and what to send.

Fig. 9 An example of 4 MPI processes, RANK0 receives data (the associated data is marked bold).¶
To receive data, RANK0 requires:
Number of MPI ranks, which will send data to RANK0 (NUMBER_OF_RECEIVERS - integer value).
Which are the MPI ranks, sending the data (RECEIVERS_RANK - integer array).
How will the received data (from each rank) be stored in the ghost vector (RECEIVERS_INDEX_OFFSET - integer array). In this example, the first 30 elements will be received from P1 \([0, 2)\) and the second 30 from P2 \([2, 4)\).
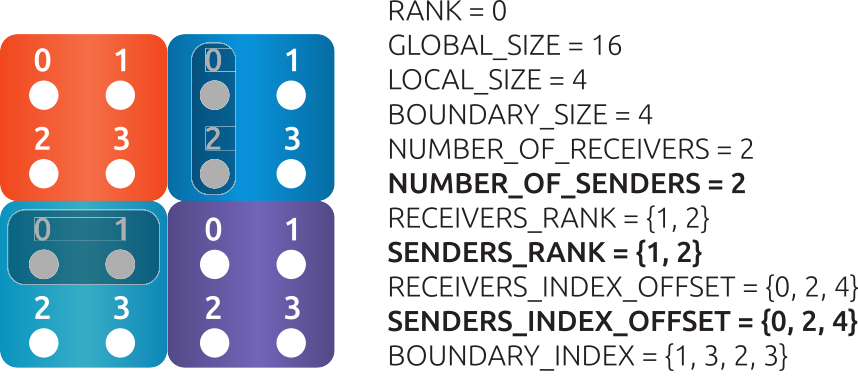
Fig. 10 An example of 4 MPI processes, RANK0 sends data (the associated data is marked bold).¶
To send data, RANK0 requires:
Total size of the sending information (BOUNDARY_SIZE - integer value).
Number of MPI ranks, which will receive data from RANK0 (NUMBER_OF_SENDERS - integer value).
Which are the MPI ranks, receiving the data (SENDERS_RANK - integer array).
How will the sending data (from each rank) be stored in the sending buffer (SENDERS_INDEX_OFFSET - integer array). In this example, the first 30 elements will be sent to P1 \([0, 2)\) and the second 30 to P2 \([2, 4)\).
The elements, which need to be send (BOUNDARY_INDEX - integer array). In this example, the data which need to be send to P1 and P2 is the ghost layer, marked as ghost P0. The vertical stripe need to be send to P1 and the horizontal stripe to P2. The numbering of local unknowns (in local indexing) for P1 (the vertical stripes) are 1, 2 (size of 2) and stored in the BOUNDARY_INDEX. After 2 elements, the elements for P2 are stored, they are 2, 3 (2 elements).
Matrices¶
Each rank hosts two local matrices, interior and ghost matrix. They can be stored in separate files, one for each matrix. The file format could be Matrix Market (MTX) or binary.
Vectors¶
Each rank holds the local interior vector only. It is stored in a single file. The file could be ASCII or binary.